Tests of General Relativity
Thesis research on this topic will involve the AEI and the Humboldt University.
In addition to the wealth of astrophysical, cosmological and nuclear physics information one can glean from gravitational wave observations, the latter are allowing us to use the coalescence of compact objects as a testing ground to unveil the fundamental nature of gravity.
So far, the general theory of relativity has passed all tests in the weak-field and low-velocity limits in the solar system and on cosmological scales, in the strong-field setting probed by binary pulsars, and in the strong-field and highly dynamical regime of BHs collision. As scientists, in order to verify general relativity, we need to find ways to falsify its alternatives. To reach this goal, we first need to make sure that our general relativity predictions are sufficiently accurate, i.e., our systematics due to modeling are smaller than statistical errors set by the signal-to-noise ratio. Then, we need to develop waveform models in modified theories of general relativity that provide us with deviations from general relativity that can be measured or bounded with gravitational wave detectors.
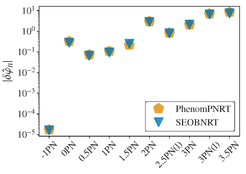
various post-Newtonian orders for GW170817. Plot produced with public code and data from https://dcc.ligo.org/LIGO-P1800059/public.
Until now general relativity deviations have been described and tested only perturbatively, as modified (or sometimes new) post-Newtonian terms in the general relativity phasing. However, general relativity deviations may not be fully captured by perturbative-like descriptions, especially during the last stages of inspiral, merger and ringdown. The NRAR modeling done for general relativity should be extended to modified theories of general relativity such as scalar-tensor theories, Einstein-Ether theory, dynamical Chern-Simons theory, Einstein-dilaton Gauss-Bonnet theory, Einstein-Maxwell-dilaton theory, etc. However, some of those theories do not have a well-posed initial-value problem (or we do not know it, yet), but this issue could be overcome by interpreting them as effective field theories or developing methods to control undesirable effects due to higher-order derivatives. Furthermore, to verify that compact objects observed by LIGO and Virgo are black holes and/or neutron stars, and not exotic objects, such as boson stars, gravastars, strange stars, etc., one would need to work out the gravitational wave predictions from those objects and compare them to the data. Also in this case the work at the interface between numerical relativity and analytical relativity will be crucial.
Graduate students in the IMPRS will tackle different projects in these relevant research topics. They could implement modified theories of general relativity (or exotic compact objects) in numerical codes, and produce waveforms for the entire process of inspiral, merger and ringdown, and use them to complete analytical, fast waveform models. They will employ those waveform models in Bayesian analysis upon gravitational wave events and verify general relativity. They could also pursue theoretical work in those modified theories of general relativity to find new phenomena and conceive ways to test them with the data. Eventually, results obtained with LIGO and Virgo for modified theories of general relativity would need to be combined with tests of those theories in the solar system, large cosmological scales and binary pulsars.
