Compact-object binary simulations

Thesis research on this topic will involve the AEI, the University of Potsdam, and the Leibniz Institute for Astrophysics.

Direct numerical solutions of the full Einstein equations have made dramatic progress during the past decade. Such simulations have explored a variety of physical scenarios which are not fully accessible by perturbative, analytical approaches.

The most important scenario is the genuinely non-linear and highly dynamic regime near the merger of two compact objects (black holes, neutron stars, or more exotic objects like boson stars): The last dozens of orbits, followed by the collision and the post-collision evolution. As member of the Simulating Extreme Spacetimes (SXS) collaboration, the AEI  participates in the development of the Spectral Einstein Code (SpEC), a multi-domain spectral code to solve Einstein’s equations. SpEC is arguably the leading code to study binary black holes. The dual-frame approach and the use of spectral methods reduce numerical dispersion and lead to very accurate simulations. Domain-decomposition techniques allow to distribute resolution efficiently, and to place the outer boundary at very large radius. Constraint preserving and minimally reflective boundary conditions further enhance the physical fidelity of solutions.

Binary black-hole simulations providing the gravitational signals near merger form an integral building block of the waveform models employed by LIGO and Virgo. The main analytical-relativity (AR) waveform model developed at the AEI-Potsdam is based on the EOB formalism (EOBNR), scientists at the AEI have also contributed to build the phenomenological inspiral-merger-ringdown model (IMRPhenom) based on extending frequency-domain post-Newtonian expressions and hybridizing EOB with numerical-relativity (NR) waveforms. Developing those NRAR models comprises three main steps: i) resum the conservative and dissipative two-body dynamics, and gravitational modes, ii) produce accurate NR simulations of compact-object binaries in a sparse region of the parameter space, and iii) calibrate the AR models against those NR waveforms, then extend them in the entire parameter space.

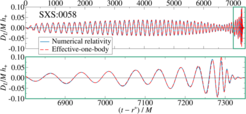
Future work on vacuum numerical relativity aims to extend the parameter space coverage of simulations. In particular binaries with very unequal masses and high spins are formidable challenges, but are essential for improving the accuracy of LIGO and Virgo template banks, and exploring the transition from comparable-mass to the extreme-mass-ratio binaries, relevant for LISA. Moreover, future gravitational wave detectors, both on the Earth and in space, will observe gravitational waves at signal-to-noise ratios exceeding 1000 (as compared to today’s signal-to-noise ratios of 30), and will therefore require simulations much more accurate than those available today, for the best possible tests of general relativity and measurement of the properties of the coalescing binaries. And finally, studies of alternative theories of gravity will add entirely new dimensions to the parameter space being studied, both in sheer size of parameter space to be covered, as well as implementation of different sets of equations governing gravity in alternative theories. These future challenges require significant improvements in the computing algorithms, to allow more robust, more efficient codes that can be applied to a wider variety of physical scenarios, and that also scale to a much larger number of compute-cores.

Graduate students in the IMPRS will use the existing numerical codes to explore the physics of coalescing binaries. They will also improve the codes, and participate in the development of new, more efficient and more scalable codes. Exploiting the unique combination of both numerical and analytical expertise, graduate students will work at the interface between NR and AR, combining, as needed, the best available frameworks (perturbation theory, EOB, NR) to understand gravitational dynamics in all regimes, and to build accurate and fast waveform models for upcoming observational runs by LIGO and Virgo, and laying foundations for LISA and 3G sources at more extreme mass-ratios.